Le rayon de Schwarschild
DĂŠfinition
Le rayon de Schwarzschild d'un trou noir est le rayon de son horizon.
Concrètement, cela signifie que si la distance entre le centre de gravitÊ G d'un "système" S (un solide, un photon, etc ...) et le centre de gravitÊ A d'un trou noir T de masse M est infÊrieure au rayon de Schwarzschild de celui-ci, S est inexorablement aspirÊ : il ne pourra plus ressortir du trou noir qu'à l'Êtat de particule, grâce au rayonnement Hawking.
DĂŠmonstration
Rappel
On a dĂŠmontrĂŠ prĂŠcĂŠdemment la relation de la vitesse de libĂŠration :
.png)
Conjecture de l'existence du rayon de Schwarzschild
Sachant que la cÊlÊritÊ de la lumière, 299 792 458 m/s est une "vitesse indÊpassable", on peut conjecturer, l'existence d'astres dont la vitesse de libÊration est supÊrieure à la cÊlÊritÊ de la lumière. Ce sont les trous noirs.
Cependant, les trous noirs sont tellement denses et massifs que leur vitesse de libĂŠration Ă la surface est bien supĂŠrieure Ă 300 * 106m/s.
Alors, pourquoi se restreindre Ă la surface ?
On va donc chercher le R "maximal", oÚ la vitesse de libÊration est exactement Êgale à la cÊlÊritÊ de la lumière. C'est le rayon de Schwarzschild.
DĂŠmonstration de la relation
Connaissant la vitesse de libĂŠration Ă trouver, 299 792 458 m/s, il ne nous reste plus qu'Ă exprimer R en fonction de M (unitĂŠes SI):
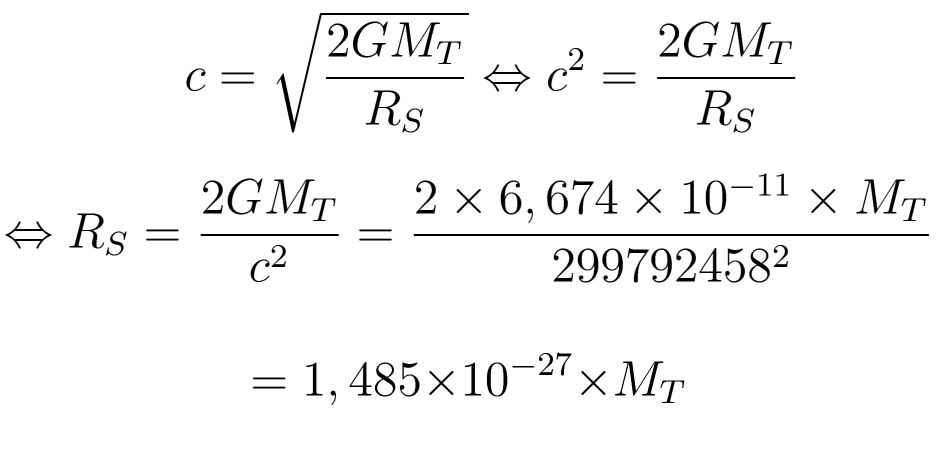
On peut tout de mĂŞme constater que ce "1,48427517 * 10-27" n'est pas des plus parlants, le kg n'ĂŠtant pas vraiment adaptĂŠ aux calculs astronomiques ... On va donc convertir M en masses solaires, unitĂŠ bien plus explicite :

Conclusion
Nous avons donc lĂ une belle relation, simple et efficace.
On peut pourtant remarquer une chose : Le rayon de Schwarzschild est ridiculement petit!
En effet, on s'aperçoit que pour chaque masse solaire supplÊmentaire, le trou noir n'augmente le rayon de son horizon que de 3 km !! Une pacotille en comparaison des 695 500 km de rayon du soleil ! Cela montre donc bien que, pour mÊriter le titre de trou noir, un astre doit être incroyablement dense, afin que son rayon de Schwarschild dÊpasse au moins le sien ...
Le "simulateur de trou noir"
Pour rendre toutes ces explications plus "tangibles", nous avons entrepris la programmation d'un "simulateur".
Derrière ce nom pompeux se cache en fait une sorte "d'expÊrience", qui aide, comme un logiciel utilisÊ en TP, à conjecturer et mettre à l'Êpreuve les formules Êtablies prÊcedemment.
Ce simulateur a ÊtÊ codÊ en Python , un langage de programmation simple et puissant. Cependant, il n'est pas intÊgrÊ par dÊfaut aux systèmes Windows. Pour utiliser le-dit simulateur, il vous faudra donc suivre les indications ci-dessous, suivant votre système d'exploitation :
- Windows : cela dĂŠpend si on a rĂŠussi Ă le "compiler".
- Mac OS : ?
- GNU/Linux : installez, s'ils ne le sont pas dÊjà , les paquets "python" et "python-qt4" (les noms peuvent lÊgèrement varier selon votre distribution).
Le code source du simulateur est accessible ici : sources